Which of the following values for the weights and the bias
would result in the final probability of the point to be
0.88 of being blue(positive region, above the line)?A. w1=2, w2=6, bias=2B. w1=3, w2=5, bias=-2.2C. w1=5, w2=4, bias=-3weights=[(2,6),(3,5),(5,4)]bias=[2,-2.2,-3]score1 = weights[0][0] * 0.4 + weights[0][1] * 0.6 + bias[0]score2 = weights[1][0] * 0.4 + weights[1][1] * 0.6 + bias[1]score3 = weights[2][0] * 0.4 + weights[2][1] * 0.6 + bias[2]def find_weights_bias(): #result of the probability function given, 0.88 with sigmoid activation 1/(1+e-score)score is 2#Find w1, w2 and b, for score=w1*0.4+w2*0.6+b weights=[(2,6),(3,5),(5,4)] bias=[2,-2.2,-3] score1 = weights[0][0] * 0.4 + weights[0][1] * 0.6 + bias[0] score2 = weights[1][0] * 0.4 + weights[1][1] * 0.6 + bias[1] score3 = weights[2][0] * 0.4 + weights[2][1] * 0.6 + bias[2] print(score1,score2,score3) #condensed form score1, score2, score3 = (w1 * 0.4 + w2 * 0.6 + b for (w1, w2), b in zip(weights, bias)) print(score1,score2,score3) if score1 == 2.0: print ("First choice is correct!") if score2 == 2.0: print ("Second choice is correct!") elif score3 == 2.0: print ("Third choice is correct!") return score1,score2,score3 find_weights_bias()
Introduction to Artificial Intelligence and Neural Nets
Thursday, January 23, 2020
Find weights and bias in neural nets in python.
Tuesday, January 21, 2020
How to use sigmoid activation function in python in basic neural nets.
The
sigmoid function is defined as sigmoid(x) = 1/(1+e-x). If the score is defined
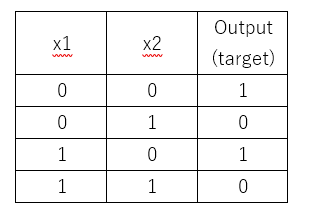
by 4x1 + 5x2 - 9 = score, then which of the following points has
exactly a 50% probability of being blue or red? (Choose all that are correct.)
- (1,1)
- (2,4)
- (5,-5)
- (-4,5)
First,
we construct a linear function to add the weights and bias term. Then, we use
activation function to return the scores to probabilities. Sigmoid function
returns values between 0 and 1.
fig1: sigmoid function
from math import e
#Equation: 4x1+5x2-9=score
#weights are 4,5 and bias is -9, find the sigmoid(x) = 1/(1+e-x).
features=[(1,1),(2,4),(5,-5),(-4,5)]
def linear_func(features):
for x in features:
score= 4*x[0]+ 5*x[1]-9
y = 1 / (1 + e - score)
print("X",x,score,y)
#call the function
linear_func(features)
#Equation: 4x1+5x2-9=score
#weights are 4,5 and bias is -9, find the sigmoid(x) = 1/(1+e-x).
features=[(1,1),(2,4),(5,-5),(-4,5)]
def linear_func(features):
for x in features:
score= 4*x[0]+ 5*x[1]-9
y = 1 / (1 + e - score)
print("X",x,score,y)
#call the function
linear_func(features)
Sunday, January 5, 2020
Training Perceptron Algorithm (Learning Rule) for Weighted NOT Logical Gates
In late 1950s Frank Rosenblatt et al. summed up the work of Warren McCulloch and Walter Pitts did about a decade earlier. McCulloch and Pitts named their discovery artificial neurons. However, there was no training method to employ this novel method which linked biological neurons to digital computing. Rosenblatt et al. named these artificial neurons, “perceptrons”, while adding a learning rule to train them to solve pattern recognition problems.
Learning rule is essentially a procedure for modifying the weights and biases of a linear equation of a neural network. A learning rule is a training algorithm that trains the perceptrons to solve specific tasks. There are many types of neural network learning rules. They are categorized as supervised learning, unsupervised learning and reinforcement (or graded) learning.
In supervised training set, the inputs and the desired targets(classes) are zipped together. The learning rule is then used to adjust the weights and biases of the network in order to fit a line (if in 1-D Cartesian space) to better classify binary output classes (make a decision boundary). The decision boundary is determined by the input vectors for which the sum of dot product of weights and inputs plus bias equals to zero (similar to a linear equation).


The key question here is, do we need to assign random weights and bias for the perceptron? Is there a rule of thumb for these values? Yes, Initially, the weights and bias of artificial neural networks must be initialized to small random numbers. This is because it is an expectation of the stochastic optimization algorithm used to train the model, called stochastic gradient descent. We want optimal weights and bias to classify accurately or get the target values correct, and stochastic gradient descent algorithm expects small random numbers as a rule of thumb. For AND Logical operator without weights, the numerical representation is given by False=0, True=1.

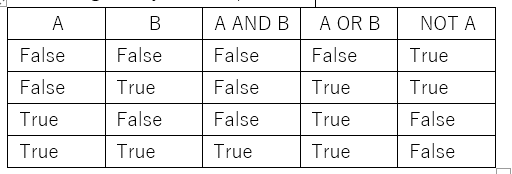
Problem: Design a perceptron based on two inputs with weights and bias to draw a correct decision boundary. Set the weights (w1, w2) and bias(b) to the values that calculate the NOT operation on the second input and ignores the first input.
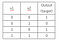
Since we want to ignore the first input, we set w1 as 0.
To solve for w2 and bias, we initialize the weight w2 as 1.0 and bias as -1.0;
For the first Row, we get:
`w2*x2+b => (1.0) *0 + (-1.0) => -1,`
As per Perceptron rule, if the predicted values is less than or equal to zero, then the sigmoid activation function transforms the negative value to zero.But the predicted value for the NOT gate is one (1), so the w2 and bias must be incorrect.we want values that will make input x2=0 to give a value of 1. Let’s keep w2=1 and change b to 1 to adjust to the output 1. The key issue here is to adjust the equation so that it equals to the predicted value for the first row.
`1(x2) + b=1=> 1*(0) + 1`, of course this value is equal to the predicted value of 1.
Second row: (keeping w2 as 1 and bias as 1)
`w2*x2+b => 1*(1)+1 => 2`
The value we got is 2, according to the learning rule, if
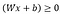
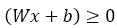
then, predicted value y-hat the sigmoid function assigns it to 1 (positive area).
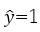
if the predicted value is less than zero, the sigmoid function assigns zero as y-hat (negative area),
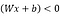
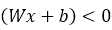
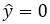
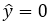
Apriori, we know that the target requires 0 for the NOT gate, so second row is incorrect. So, we need row two, x2 which is 1, to give target value of zero. If we change w2 to -1, we have;
-1*(x2) +1 => -1+1 = 0. Since the calculated value is zero, y-hat is 1,but the target value is zero. So let’s change bias, b to 0.5, to make the desired output more than zero so that y-hat is 1.
With w2=-1, and b=0.5
-1(x2) + 0.5 => -1*(0) +0.5 = 0.5, sigmoid activation function outputs of positive values gives predicted value of 1. So, this fits the desired target. Checking third row and fourth row shows the solution is valid too.
For the third row,
`-1(x2) + (-0.5) => (-1*0)+0.5 => 0.5`
For the fourth row:
`-1(x2) + (0.5) => (-1*1)+0.5 => 1.5`
As a novice in AI, please if you find any grand errors, let me know. The method seemed an arbitrary search of values to me. So, I looked for reference and got the following perceptron learning rule, whatever that meant. The notations are scary!
import pandas as pd#NOT Operator# TODO: Set weight1, weight2, and biasweight1 = 0.0weight2 = -1.0bias = 0.5# DON'T CHANGE ANYTHING BELOW# Inputs and outputstest_inputs = [(0, 0), (0, 1), (1, 0), (1, 1)]correct_outputs = [True, False, True, False]outputs = []# Generate and check outputfor test_input, correct_output in zip(test_inputs, correct_outputs):linear_combination = weight1 * test_input[0] + weight2 * test_input[1] + biasoutput = int(linear_combination >= 0)is_correct_string = 'Yes' if output == correct_output else 'No'outputs.append([test_input[0], test_input[1], linear_combination, output, is_correct_string])# Print outputnum_wrong = len([output[4] for output in outputs if output[4] == 'No'])output_frame = pd.DataFrame(outputs, columns=['Input 1', ' Input 2', ' Linear Combination', ' Activation Output', ' Is Correct'])if not num_wrong:print('Nice! You got it all correct.\n')else:print('You got {} wrong. Keep trying!\n'.format(num_wrong))print(output_frame.to_string(index=False))


Reference:
Lecture 2: Single Layer Perceptrons, Kevin Swingler, kms@cs.stir.ac.uk
Subscribe to:
Comments (Atom)

